Transparent, standards-aligned explanations of the methodologies behind our personal rate of return metrics.
Personal rate of return measures an individual’s investment performance using their specific transaction history and cash flows. This section details the standards and methodologies for time- and dollar-weighted return calculations.
A time-weighted rate of return (“TWRR”) takes into account the length of time an investor has been invested in a given security, such as a stock, bond, or mutual fund. It measures how effectively the invested dollars have grown over time. Cash flows into and out of the investment do not affect the time-weighted rate of return, unlike the dollar-weighted rate of return, or “IRR,” which is influenced by the timing and amount of cash flows.
Time-weighted rates of return can be calculated on a daily basis using a method known as Daily Valuation, or by using a slightly less accurate—but in some cases more convenient—monthly method known as Modified Dietz, in which inflows and outflows are averaged over the month. These time-weighted calculation methods provide a truer measure of underlying investment performance.
When no cash flows are present, total return for a given period is calculated using the following equation:
…where EMV is the market value of the asset at the end of the period, including any accrued income, and BMV is the market value of the asset at the beginning of the period.
When cash flows are present, dailyVest uses the Modified Dietz approximation method. The TWRR – Modified Dietz method provides an approximate time-weighted return, whereas the TWRR – Daily Valuation method produces a true time-weighted return. TWRR – Modified Dietz uses the beginning and ending portfolio values for the month and weights each cash flow (contribution or withdrawal) based on the length of time it is invested. The resulting monthly portfolio returns are then geometrically linked to derive quarterly or annual returns.
The formula for estimating the time-weighted rate of return using the Modified Dietz method is:
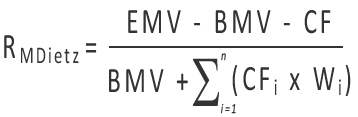
…where EMV is the market value of the portfolio at the end of the period, including all income accrued through the end of the period; BMV is the portfolio’s market value at the beginning of the period, including all income accrued through the end of the previous period; and CF represents the net cash flows during the period. Contributions to the portfolio are treated as positive cash flows (“inflows”), while withdrawals or distributions are treated as negative cash flows (“outflows”).
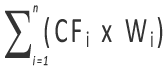
The equation above represents the sum of each cash flow, CFi, multiplied by its corresponding weight, Wi. The weight Wi represents the proportion of the total number of days in the period that cash flow CFi has been held in (or out of) the portfolio. The formula for Wi is:
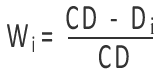
…where CD is the total number of calendar days in the period and Di is the number of calendar days since the beginning of the period on which cash flow CFi occurred. The numerator assumes that the cash flows occur at the end of the day.
For example, if a cash flow occurred on January 20 and the month of January has 31 days, the weight Wi is then calculated as:
(31–20)/31 = 0.35483871
After computing monthly returns, they are geometrically linked to produce a quarterly return using the following formula:
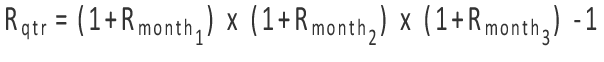
…where Rqtr is the portfolio’s quarterly return, and Rmonth1, Rmonth2, and Rmonth3 are the returns for months 1, 2, and 3, respectively.
Similarly, the annual rate of return may be calculated by geometrically linking quarterly portfolio returns using the following formula:
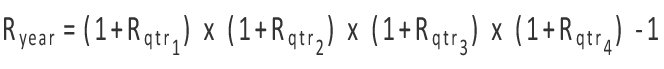
…where Rqtr1, Rqtr2, Rqtr3, and Rqtr4 are the returns for quarters 1, 2, 3, and 4, respectively. Alternatively, the annual return can be calculated by geometrically linking all twelve monthly returns.
The primary advantage of the Modified Dietz method is that it does not require portfolio valuation on the date of each cash flow. This was historically beneficial for older systems that lacked the ability to produce daily valuations for all holdings. Its primary disadvantage is that it provides a less accurate approximation of the true time-weighted rate of return. This inaccuracy is most pronounced when one or more of the following conditions exists:
Note that the Modified Dietz approximation method has not conformed to the GIPS® standards since January 1, 2010. Although Modified Dietz is only slightly less accurate than the Daily Valuation method, the primary motivation for this non-conformance was to ensure that the GIPS® standards keep pace with modern technology. Today, valuing portfolio holdings at the time of external cash flows requires little additional effort—not only on a daily basis, but in some cases in real-time. The Daily Valuation method is therefore not only the most accurate approach, but also ideally suited for systems that value assets daily.
Performing an actual valuation of each holding, account, or entire portfolio at the time of every external cash flow produces the most accurate time-weighted rate of return (TWRR). In practice, this requires the ability to obtain daily valuations for all portfolio holdings on a continuous basis—a capability that is standard in most modern systems.
Returns calculated under these conditions use the Daily Valuation Method, which produces a true TWRR rather than an estimate. This method divides the overall performance period into sub-periods, with boundaries determined by the occurrence of external cash flows. The formula for calculating a sub-period return is:
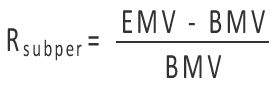
…where EMV is the market value of the portfolio at the end of the sub-period, before any cash flows during that period, but including accrued income for the sub-period. BMV is the market value at the end of the previous sub-period (that is, the beginning of the current sub-period), including any cash flows at the end of the previous sub-period and all accrued income through the end of that period.
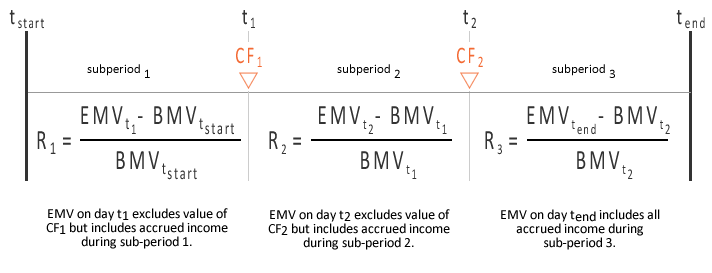
The boundaries of these sub-periods can be illustrated by an example containing two cash flows, CF1 and CF2.
The resulting sub-period returns (for example, R1, R2, R3) are then geometrically linked using the following formula:
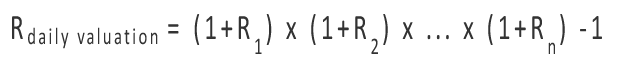
…where Rdaily valuation is the total return calculated using the Daily Valuation Method, and R1, R2 … Rn are the returns for sub-periods 1 through n, respectively.
Sub-period 1 extends from the first day of the overall period up to and including the date of the first cash flow, excluding the value of that cash flow but including all accrued income for the sub-period. Sub-period 2 begins the following day and extends through the date of the second cash flow, again excluding the value of that cash flow but including accrued income. This pattern continues for each subsequent cash flow. The final sub-period extends from the day of the last cash flow through the final day of the overall period.
Based on the sub-period boundaries defined above, this method assumes that a cash flow is not available for investment until the beginning of the next day. Accordingly, when the portfolio is valued on the date of a cash flow, the cash flow is not reflected in the Ending Market Value for that day. Instead, it is added to determine the Beginning Market Value for the following day.
The primary advantage of this method is that it calculates the true time-weighted rate of return, rather than an approximation as with the Modified Dietz method. The primary disadvantage is that it requires daily valuation of all portfolio holdings, which may increase data and processing demands.
The dollar-weighted rate of return (“DWRR”), also known as the money-weighted rate of return and the internal rate of return—more commonly referred to as “IRR”—is used to determine the rate of return on an investment. IRR equates the present value of an investment’s cash inflows (such as dividends, interest, and sales proceeds) with the present cost of the investment.
For an investment that generates a series of cash flows over time, the IRR is defined as the discount rate that causes the net present value of those cash flows equal to zero. Stated another way, the IRR is:
“…the interest rate that will make the present value of the cash flows from all the sub-periods in the evaluation period plus the terminal market value of the portfolio equal to the initial market value of the portfolio.”
GIPS® (formerly AIMR-PPS) requires the calculation of a time-weighted rate of return, which takes into account both cash flows and the market value of assets at the beginning and end of each period. dailyVest performs monthly valuations using the Modified Dietz method, which does not require daily valuations—although daily valuations are available for the majority of our clients.
The Modified Dietz method uses beginning and ending asset values for the period and weights each cash flow by the amount of time it is invested during that period. Consistent with GIPS® recommendations, dailyVest defines a “cash flow” as an external flow of cash and/or securities (capital additions or withdrawals) initiated by the investor. Reinvested income is not considered a cash flow; instead, it represents appreciation or depreciation in the value of the portfolio and is incorporated into the calculation of historical beginning and ending sub-period market values.
According to the GIPS® website, “The GIPS standards are a set of ethical principles used by investment management firms in order to establish a globally standardized, industry-wide approach to creating performance presentations that communicate investment results to prospective clients.”
Full GIPS® compliance is composed of many components, of which calculation methodology is only one. dailyVest does not claim full GIPS® compliance, but rather follows certain guidelines within the standard related specifically to calculation methodology.
PLEASE NOTE: The information presented in this section, as well as the performance reporting available through dailyVest software, is based solely on calculation methods derived from guidelines established by the Investment Performance Council of the CFA Institute (formerly the Association for Investment Management and Research, AIMR) in its Global Investment Performance Standard (GIPS®) handbook.
dailyVest does not claim compliance with GIPS®, as only firms that manage assets are eligible to claim compliance. Furthermore, the Investment Performance Council of the CFA Institute has not been involved in the preparation or review of these notes, nor has it had any involvement with dailyVest.